§7.6 空间曲线及其方程
一
空间曲线的一般方程
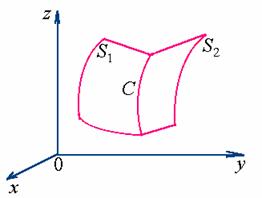
空间曲线可看作两曲面的交线,设
![]() 和
和 ![]()
是两曲面的方程,它们的交线为![]() 。曲线上的任何点的坐标
。曲线上的任何点的坐标![]() 应同时满足这两个曲面方程,因此,应满足方程组
应同时满足这两个曲面方程,因此,应满足方程组
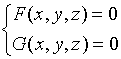 (1)
(1)
反过来,如果点![]() 不在曲线
不在曲线![]() 上,那么它不可能同时两曲面上。所以,它的坐标不满足方程组(1)。由上述两点可知:曲线
上,那么它不可能同时两曲面上。所以,它的坐标不满足方程组(1)。由上述两点可知:曲线![]() 可由方程组(1)表示。
可由方程组(1)表示。
方程组(1)称作空间曲线的一般方程。
二 空间曲线的参数方程
对于空间曲线![]() , 若
, 若![]() 上的动点的坐标
上的动点的坐标![]() 可表示成为参数
可表示成为参数![]() 的函数
的函数
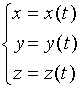 (2)
(2)
随着![]() 的变动可得到曲线
的变动可得到曲线![]() 上的全部点,方程组(2)叫做空间曲线参数方程。
上的全部点,方程组(2)叫做空间曲线参数方程。
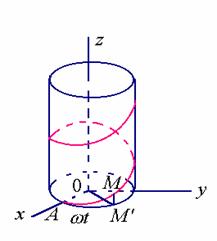
【例1】如果空间一点![]() 在圆柱面
在圆柱面![]() 上以角速度
上以角速度![]() 绕
绕![]() 轴旋转,同时又以线速度
轴旋转,同时又以线速度![]() 沿平行于
沿平行于![]() 轴的正方向上升(其中:
轴的正方向上升(其中:![]() ,
,![]() 均为常数),那未点
均为常数),那未点![]() 的轨迹叫做螺旋线,试建立其参数方程。
的轨迹叫做螺旋线,试建立其参数方程。
解:取时间![]() 为参数。
为参数。
设当
![]() 时,动点与
时,动点与![]() 轴上的点
轴上的点 ![]() 重合,经过时间
重合,经过时间![]() ,动点由
,动点由![]() 运动到
运动到![]() 。 记
。 记![]() 在
在![]() 面上的投影为
面上的投影为![]() ,它的坐标为
,它的坐标为![]() 。
。
由于动点在圆柱面上以角速度![]() 绕
绕![]() 轴旋转,经过时间
轴旋转,经过时间![]() ,
,![]()
从而 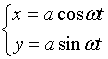
又由于动点同时以线速度![]() 沿平行于
沿平行于![]() 轴正方向上升,所以
轴正方向上升,所以
![]()
因此,螺旋线的参数方程为
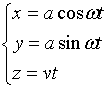
或令![]() ,则方程形式可化为
,则方程形式可化为

螺旋线有一个重要性质:
当![]() 从
从![]() 变到
变到![]() 时,
时,![]() 由
由![]() 变到
变到![]() ;这表明当
;这表明当![]() 转过角
转过角![]() 时,
时,![]() 点沿螺旋线上升了高度
点沿螺旋线上升了高度![]() ;
;
特别地,当![]() 转过一周,即
转过一周,即![]() 时,
时,![]() 点就上升固定的高度为
点就上升固定的高度为![]() ,这个高度在工程技术上叫螺距。
,这个高度在工程技术上叫螺距。
空间曲线的一般方程也可以化为参数方程,下面通过例子来介绍其处理方法。
【例2】将空间曲线![]()
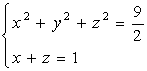 表示成参数方程。
表示成参数方程。
解:由方程组消去![]() 得
得
![]()
![]()
![]()
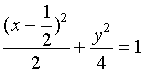
由于![]() 在此椭圆柱面上,故
在此椭圆柱面上,故![]() 的方程可用如下形式来表示
的方程可用如下形式来表示
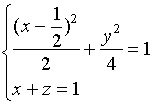
(1)、如果我们以![]() 作为参数,即令
作为参数,即令 ![]()
则 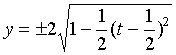
![]()
从而得到曲线的参数方程
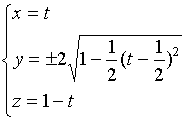
且参数的取值范围为
![]()
![]()
(2)、如果令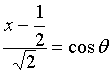 ,由椭球柱面方程有
,由椭球柱面方程有 ![]() ,而
,而
![]()
则曲线又可表示成为
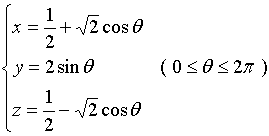
一般来说:
1、空间曲线总可以用参数形式给出它的方程;
2、随着参数选取的不同,方程的形式会发生变化。
三
空间曲线在坐标面上的投影
设空间曲线![]() 的一般方程为
的一般方程为
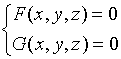 (1)
(1)
下面,我们来研究由方程组(1)消去变量![]() 之后所得到的方程
之后所得到的方程
![]() (2)
(2)
因(2)是由(1)消去![]() 后所得,则当坐标
后所得,则当坐标 ![]() 适合方程组(1)时,前两个坐标
适合方程组(1)时,前两个坐标![]() 必定适合方程(2),即曲线
必定适合方程(2),即曲线![]() 上的所有点都在由(2)表示的曲面上。
上的所有点都在由(2)表示的曲面上。
而方程(2)表示一个母线平行于![]() 轴的柱面,因此,此柱面必定包含曲线
轴的柱面,因此,此柱面必定包含曲线![]() 。以曲线
。以曲线![]() 为准线,母线平行于
为准线,母线平行于![]() 轴的柱面叫做关于
轴的柱面叫做关于![]() 面的投影柱面;
面的投影柱面;
投影柱面与![]() 面的交线叫做空间曲线
面的交线叫做空间曲线![]() 在
在![]() 面上的投影曲线,该曲线的方程可写成
面上的投影曲线,该曲线的方程可写成
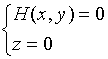
同理,消去方程组( 1) 中的变量
![]() 或
或 ![]() ,再分别与
,再分别与 ![]() 或
或 ![]() 联立,我们便得到了空间曲线
联立,我们便得到了空间曲线![]() 在
在 ![]() 或
或 ![]() 面上的投影曲线方程。
面上的投影曲线方程。
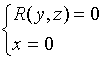 或
或 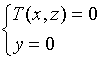
【例3】求曲线![]()
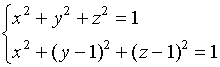
在![]() 面上的投影曲线方程。
面上的投影曲线方程。
解:先求包含曲线![]() 且母线平行于
且母线平行于![]() 轴的柱面,从方程组
轴的柱面,从方程组
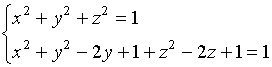
中消去![]() ,有
,有
![]()
以![]() 代入方程组中第一个方程得到
代入方程组中第一个方程得到
![]()
这便是所要求的柱面方程。
于是,曲线![]() 在
在![]() 面上的投影曲线为
面上的投影曲线为

有时,我们需要确定一个空间立体(或空间曲面)在坐标面上的投影,一般来说,这种投影往往是一个平面区域,因此,我们称它为空间立体(或空间曲面)在坐标面上的投影区域。
投影区域可以利用投影柱面与投影曲线来确定。
【例4】求上半球面 ![]() 和锥面
和锥面 ![]() 所围成的空间立体
所围成的空间立体![]() 在
在![]() 面上的投影区域
面上的投影区域![]() 。
。
解:上半球面与锥面的交线为
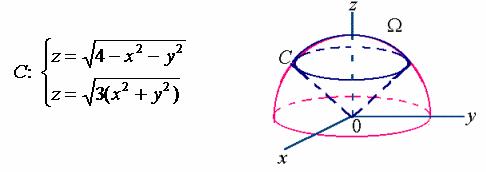
由方程组消去变量![]() ,有
,有
![]()
这是母线平行于![]() 轴的投影柱面,空间立体
轴的投影柱面,空间立体![]() 恰好镶在该柱体内,该柱体在
恰好镶在该柱体内,该柱体在![]() 面的交线所包围的区域正好是
面的交线所包围的区域正好是![]() 在
在![]() 面上的投影区域
面上的投影区域![]() 。
。
投影柱面在![]() 面上的交线为
面上的交线为
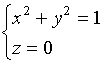
这是一个圆,它所包围的区域为![]() 。
。